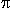Tetrahedral Geodesics

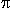David Anderson
Originally written in June 1998

Since an icosahedron approximates a sphere closely at the onset, most people associate geodesics with icosahedral structure. But geodesic properties are not limited to the tesselated icosaheron. From my perspective, any de-projection of a sphere onto a closed solid can be consided geodesic; any form will do.

I decided to explore the ins and outs of tetrahedral geodesic structure. Although globally, the tetrahedron is less complex than the icosahedron, the projective mathematics of the transformation is identical. And the form of the resulting geodesic looks quite bizarre.

To make a tetrahedral geodesic patch, the first goal is understanding a tetrahedron analytically. A tetrahedron is the simplest of the platonic solids. Four equilateral triangles are edge-connected to form a three-sided pyramid with a triangular base. The center of the solid lies equidistant from each vertex; the solid is rotationally symmetic around any center-vertex and center-face axis with a period of 2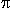/3, and rotationally symmetric around any center-edge axis with a period of .

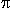The neatest trick (and the easiest way) I've seen to construct at tetrahedron is with a cube. 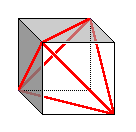By connecting the opposite corners of opposite faces, a perfect tetrahedron is formed. How can you tell? Because the length of all the edges is the same (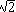 in a unit cube) and the distance from any vertex to the center is the same (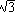/2 in a unit cube.) This makes the center of the cube the center of the tetrahedron. Now, if we choose to deal with the unit tetrahedron we need to scale everything by 1/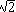: the edges become one unit long and the distance from the center to a vertex becomes /.

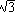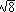To make a tetrahedral geodesic patch along the lines of what we've done before for the icosahedron, we need to situate a triangular mesh of points in 3-space, with the top vertex on the z-axis and the bottom two vertices symmetric, the same distance from but on opposite sides of the x axis. Therefore, we know the top vertex is (0,0,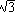/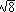), but the bottom vertices, (x₁,y₁,z₁) and (x₂,y₂,z₂), are unknown.

We can make three mathematical statements about the vertices of our mesh:

1. From symmetry, x₁ = x₂, y₁ = -y₂, and z₁ = z₂

2. The distance between any two vertices is the length of an edge, ((x_a - x_b)² + (y_a - y_b)² + (z_a - z_b)²)^1/2 = 1

3. The distance from the tetrahedron's center (0,0,0) to any vertex is known, (x_a² + y_a² + z_a²)^1/2 = /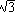

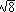
This turns out to be enough information enough to find the unknown vertices. Substituting 1 into 2, we have:

((2y₁)²)^1/2 = 1

which fixes y₁ at 1/2 and y₂ at -1/2. Knowing this makes equation 3 for the first unknown point become:

(x₁² + 1/4 + z₁²)^1/2 = /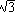

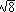
By using this information with the distance from the first unknown vertex to the top vertex we have:

(x₁² + 1/4 + (z₁ - 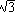/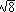)²)^1/2 = 1

These two equations can now be solved simultaneously to find that x₁ = 1/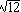 and z₁ = -1/.

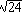Our mesh vertices are (0,0,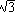/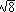), (1/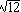,1/2,-1/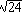) and (1/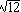,-1/2,-1/).

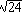Now that the mesh can be constructed, a simple change to the previous program that generated a vrml icosahedral geodesic patch world and merger with the other previous program that which generated an html icosahedral geodesic patch table of vertices and chord lengths yields a new gd.coffee. This code will generate a tetrahedral patch rendered as html tables as well as a vrml world. And, since it was already there, the octet truss bracing is also included. The color coding of the struts in vrml matches the coding described in the previous paper.

For example, the outer shell of a 5-frequency tetrahedral geodesic patch with a side length of 1 unit is rendered as:

Vertices

Vertex	x	y	z
(0,0)	0	0	1
(0,1)	0.12451	-0.21567	0.9685
(1,0)	0.12451	0.21567	0.9685
(0,2)	0.31427	-0.54433	0.77778
(1,1)	0.37463	0	0.92717
(2,0)	0.31427	0.54433	0.77778
(0,3)	0.4714	-0.8165	0.33333
(1,2)	0.73855	-0.4264	0.52223
(2,1)	0.73855	0.4264	0.52223
(3,0)	0.4714	0.8165	0.33333
(0,4)	0.49806	-0.86266	-0.08805
(1,3)	0.74927	-0.64889	-0.13245
(2,2)	0.98473	0	-0.17408
(3,1)	0.74927	0.64889	-0.13245
(4,0)	0.49806	0.86266	-0.08805
(0,5)	0.4714	-0.8165	-0.33333
(1,4)	0.62257	-0.647	-0.44023
(2,3)	0.78567	-0.27217	-0.55556
(3,2)	0.78567	0.27217	-0.55556
(4,1)	0.62257	0.647	-0.44023
(5,0)	0.4714	0.8165	-0.33333

Chord Lengths

Chords	Count	Length
(0,0)-(0,1) (0,0)-(1,0) (0,4)-(0,5) (0,5)-(1,4) (4,0)-(5,0) (4,1)-(5,0)	6	0.25101
(0,1)-(1,1) (1,0)-(1,1) (0,4)-(1,3) (3,1)-(4,0) (1,3)-(1,4) (3,1)-(4,1)	6	0.33284
(0,1)-(0,2) (1,0)-(2,0) (0,3)-(0,4) (3,0)-(4,0) (1,4)-(2,3) (3,2)-(4,1)	6	0.42474
(0,1)-(1,0) (0,4)-(1,4) (4,0)-(4,1)	3	0.43133
(0,2)-(1,2) (0,3)-(1,2) (2,0)-(2,1) (2,1)-(3,0) (2,2)-(2,3) (2,2)-(3,2)	6	0.50914
(0,2)-(0,3) (2,0)-(3,0) (2,3)-(3,2)	3	0.54433
(0,2)-(1,1) (1,1)-(2,0) (0,3)-(1,3) (3,0)-(3,1) (1,3)-(2,3) (3,1)-(3,2)	6	0.56768
(1,1)-(1,2) (1,1)-(2,1) (1,2)-(1,3) (1,3)-(2,2) (2,1)-(3,1) (2,2)-(3,1)	6	0.69154
(1,2)-(2,1) (1,2)-(2,2) (2,1)-(2,2)	3	0.8528

The vrml world for this example displays a patch which looks like this:

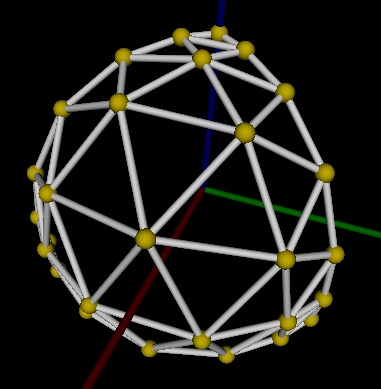
At this point I'm constructing a small 6-frequency tetrahedral geodesic sphere out of pipe cleaners and coffee stirrers to hang on the wall.

The interesting thing to note about the tetrahedral geodesic is the seeming unevenness of the projection. Since the unprojected points in the mesh near center of a face are so much closer to the center of the solid, they must be projected farther to lie on the circumscribed sphere. These points end up farther apart the farther they're projected and the tesselations of the side are smaller near edges and larger near the center of a face. The geodesic grid looks distorted - like it's bulging too far outward. Of course, bulging is present in all tesselations of a flat surface onto a sphere; but since a quarter of the sphere's surface area is covered by each patch, the bulge is much more pronounced - in a sense, the bulging of the projected tetrahedral is five times more pronounced than the projected side of an icosahedron.

What this pronounced bulging implies for building domes is a much larger varience of struts sizes in the tetrahedral geodesic than the icosahedral geodesic. With icosahedral geodesics, since the bulge in a projected side is smaller, chord lengths have less variance and tesselations are closer in size. However, in tetrahedral geodesics, the tesselations are relatively small near the vertics and grow larger as the center of the side is approaced. The short struts are the edges of the smaller tesselations; the longer struts are edges of the larger tesselations.

We can take advantage of this bulging. A small tetrahedral geodesic could be used as a simple temporary shelter. If three odd-frequency patches were used, a tetrahedral geodesic dome cold be constructed with entry through the largest triangle in one of the patch tesselations, and large transparent windows in the others. These shelters would still approximate a spherical shape, with all the economies that come with it, but for significantly fewer parts than a full scale icosahedral geodesic. In addition, since there is be more variance between the parts, there'd be less chance of mis-construction. Larger tetrahedral geodesics would also offer some economy, and could be linked to icosahedral geodesics to offer some variation. (To say nothing of the middle ground of octahedral geodesics - which is next.)

However as in all geodesics, as the frequency increases the local variance of the parts decreases. And because of the eveness of the projection, a icosahedral geodesic will always more closely approximate a sphere than a tetrahedral geodesic for a given frequency. If a more-perfect, more-uniformally-tesselated sphere is what's desired, the tetrahedron loses. But in a world which is always seeking novelty, the tetrahedral geodesic structure is certainly different, and certainly fun to play with.