
Planning a Bigger Dome, Part II
David Anderson
Originally written in May 1998
To build a good support structure based on an octet truss, the notion of separate inner and outer shells is simply a convenience.
In Part I, a 10-frequency outer icosahedral shell was considered to be supported by a 9-frequency inner icosahedral shell connected by a system of struts.
These struts connect the shells together to form a layer of tetrahedrons and octahedrons.
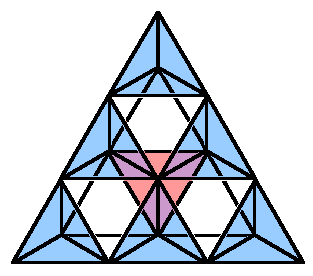 A section of this layering can be seen in the diagram on the left.
Downward pointing tetrahedrons are blue, while the upward pointing tetrahedrons are red.
(Although only one upward pointing tetrahedron is shown, look closely at the arrangement and extend it outward.
You ought to get the idea...)
The volumes between these tetrahedrons are octahedrons.
This space-filling arrangement is a section of an octet truss.
When this structure is appropriately extended and its vertices are projected as an icosahedral patch, the resulting shell reinforces itself radially to resist local deformations.
A section of this layering can be seen in the diagram on the left.
Downward pointing tetrahedrons are blue, while the upward pointing tetrahedrons are red.
(Although only one upward pointing tetrahedron is shown, look closely at the arrangement and extend it outward.
You ought to get the idea...)
The volumes between these tetrahedrons are octahedrons.
This space-filling arrangement is a section of an octet truss.
When this structure is appropriately extended and its vertices are projected as an icosahedral patch, the resulting shell reinforces itself radially to resist local deformations.
To calculate the vertices of this puppy for use in a geodesic, you have to find the centers of every other tesselation on the geodesic patch and project them only to a fraction of the radius of the circumscribed sphere.
This can be computed easily if the tesselation is effectively calculated at three times the frequency with the extra unused vertices discarded.
Triple the frequency, you ask?
Why not double?
Consider: if you double the frequency, you end up with four triangles - the new vertices are on the edges, not in the face.
Only if you triple (or tesselate with a frequency that has a factor of 3 in it) does the center point get calculated explicitly.
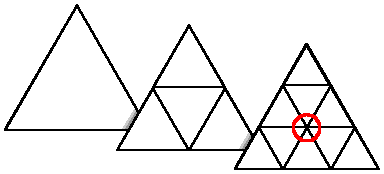 (In the diagram on the right, the red circle indicates the center of the face.)
The nicest part about all this is that most of the calculations needed can be made by adapting the techniques which were previously determined for calculating chord lengths for a geodesic patch.
The code adjustments are straightforward.
(In the diagram on the right, the red circle indicates the center of the face.)
The nicest part about all this is that most of the calculations needed can be made by adapting the techniques which were previously determined for calculating chord lengths for a geodesic patch.
The code adjustments are straightforward.
The only tricky part of this is what the fraction of the radius to project the center point should be.
And this turns out to be only a little nasty...
In order to utilize the octet truss in a geodesic patch, it has to be deformed.
The tetrahedrons' sides are stretched - the further their vertices have to be projected from the "truss plane", the greater the stretch.
To preserve the maximum strength of the tetrahedron in the truss, the radial distance of the center vertex must be multiplied by the relative change of the radial projection to the circumscribed sphere.
First we assume the triangle's center vertex is on the patch so we can generate the relative change: (r+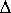 r)/r.
r)/r.
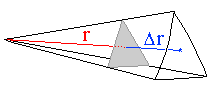 Now we must consider that on an unprojected side, the center point already lies "below" the face by the altitude of the tetrahedron - call its radial distance h, equal to the altitude of the tetrahedron.
So when we put it together, the new radial distance for the vertex is then h(r+
Now we must consider that on an unprojected side, the center point already lies "below" the face by the altitude of the tetrahedron - call its radial distance h, equal to the altitude of the tetrahedron.
So when we put it together, the new radial distance for the vertex is then h(r+ r)/r.
All that's left is a little math to figure out the value of r - which we already have by simply converting Cartesian to Spherical coordinates.
Generally, the sides of the tetrahedron will be longer in the center of an icosahedral side, where the projected distance is greatest.
r)/r.
All that's left is a little math to figure out the value of r - which we already have by simply converting Cartesian to Spherical coordinates.
Generally, the sides of the tetrahedron will be longer in the center of an icosahedral side, where the projected distance is greatest.
Of course, we could ditch all this complication and simply subtract a constant amount from each radial distance for points on the inner shell, and everything would likely work out well enough.
But as the domes get bigger and the structural integrity is brought into question, I'd rather follow the all rules that I can figure out.
The last thing which has to be done is to connect the inner shells.
Since each side-structure of the geodesic has an underlying shell which is recessed by "half" a subface width, although the sides of the outer shell meet at geodesic vertices, the sides of the inner shell must be connected artificially.
The edge vertices of the inner shell are connected to their neighbors by a "ladder" of struts.
The chordlength application from the earlier paper has now been adapted to generate the inner shell and extra chords for an arbitrary size and frequency:
Finally, here are the chord lengths for a patch of the 50 ft diameter dome.
If I can engineer in a few walkways, find some financing and able bodies, and a suitable place to build it, it'd be a really cool project...
 A section of this layering can be seen in the diagram on the left.
Downward pointing tetrahedrons are blue, while the upward pointing tetrahedrons are red.
(Although only one upward pointing tetrahedron is shown, look closely at the arrangement and extend it outward.
You ought to get the idea...)
The volumes between these tetrahedrons are octahedrons.
This space-filling arrangement is a section of an octet truss.
When this structure is appropriately extended and its vertices are projected as an icosahedral patch, the resulting shell reinforces itself radially to resist local deformations.
A section of this layering can be seen in the diagram on the left.
Downward pointing tetrahedrons are blue, while the upward pointing tetrahedrons are red.
(Although only one upward pointing tetrahedron is shown, look closely at the arrangement and extend it outward.
You ought to get the idea...)
The volumes between these tetrahedrons are octahedrons.
This space-filling arrangement is a section of an octet truss.
When this structure is appropriately extended and its vertices are projected as an icosahedral patch, the resulting shell reinforces itself radially to resist local deformations.

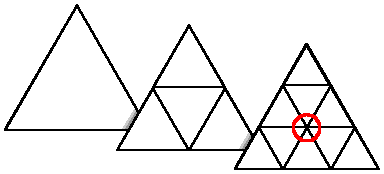 (In the diagram on the right, the red circle indicates the center of the face.)
The nicest part about all this is that most of the calculations needed can be made by adapting the techniques which were previously determined for calculating chord lengths for a geodesic patch.
The code adjustments are straightforward.
(In the diagram on the right, the red circle indicates the center of the face.)
The nicest part about all this is that most of the calculations needed can be made by adapting the techniques which were previously determined for calculating chord lengths for a geodesic patch.
The code adjustments are straightforward.
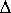 r)/r.
r)/r.
 Now we must consider that on an unprojected side, the center point already lies "below" the face by the altitude of the tetrahedron - call its radial distance h, equal to the altitude of the tetrahedron.
So when we put it together, the new radial distance for the vertex is then h(r+
Now we must consider that on an unprojected side, the center point already lies "below" the face by the altitude of the tetrahedron - call its radial distance h, equal to the altitude of the tetrahedron.
So when we put it together, the new radial distance for the vertex is then h(r+