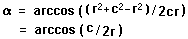Calculating Geodesic Radial Vertex Angles

David Anderson
Originally written in April 1999

One of the calculations I've neglected to this point is the angle at a vertex between the center of the circumscribed sphere and it's neighboring vertices. This is not a complex calculation, especially given all the things that we've been through in some of the other papers, but it used in the creation of the hubs used in many popular geodesic designs.

Each hub in the geodesic structure points to different set of vertices and is potentially different - we know the angles between the vertices, but not the angles that adjust the direction below the normal plane at the vertex on the radial line from the center.

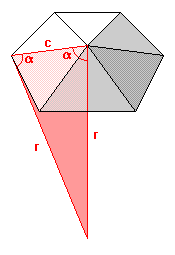Given the radius and chord length between vertices, we have an isoceles triangle; the distance between the vertices is the base, the distances between each vertex and the center is the radius. We can find the angle easily using the law of cosines:

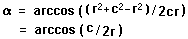
This angle is the same at each vertex of the chord, of course, in accordance with the nature of the isoceles triangle.

Because this paper is so short, and because I just love to write code, I decided to do it some justice by adapting the code to produce tables of radial angles. These angles are independent of the size of the geodesic - as are all angles. The calculation merely depends on the frequency of the geodesic and the choice of underlying Platonic solid.

The gd.coffee program will calculate the radial angles for all the hubs in an n-frequency patch of a given geodesic type (tetrahedral, octahedral, or icosahedral.) The values for the first five frequencies of each type are precomputed for your convenience.