 . All done.
. All done.

David Anderson
Originally written in June 1998
To round out the tessellation of platonic solids made up of equilateral triangles, attention is briefly turned to the octahedron. The tessellation of an octahedron is done in the same way as the icosahedron and the tetrahedron and has similar properties. But it also has some different properties - ones that make it considerably more attractive as a bridge between traditional, right-angle construction and the more resource-efficient geodesics.
To make a octahedral geodesic patch, the octahedron must be analytically understood. The octahedron is a middle ground between the tetrahedron and the icosahedron. In a tetrahedron, three equilateral triangles come together at a vertex; in an icosahedron, five. The octahedron has four equilaterals coming together at each vertex.
To tessellate an octahedral side, the vertices of the side must be found. This is quite easy; for a unit icosahedron with a center at (0,0,0), the six vertices lie on the 3D axis at (v,0,0), (-v,0,0), (0,v,0), (0,-v,0), (0,0,v), and (0,0,-v). to find v, all is needed is that the distance between two adjacent vertices must equal one:
(v2 + v2)1/2 = 1
which fixes v at 1/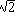 . All done.
. All done.
Adding octahedral geodesics to the previous tetrahedral and icosahedral generating code gives us gd.coffee. This generates an octahedral patch rendered as html tables and a vrml world (with an obligatory octet truss.) Again, the color coding of the struts in vrml matches the coding described in the supporting truss paper, and the designators mean g: geodesic hub and i: inner truss hub.
For example, the outer shell of a 10-frequency octahedral geodesic patch with a side length of 3 unit is rendered as (octet truss removed for brevity):
| Vertex | x | y | z |
| (g:0,0) | 0 | 0 | 3 |
| (g:0,1) | 0.23426 | -0.23426 | 2.98165 |
| (g:1,0) | 0.23426 | 0.23426 | 2.98165 |
| (g:0,2) | 0.5145 | -0.5145 | 2.91043 |
| (g:1,1) | 0.52223 | 0 | 2.9542 |
| (g:2,0) | 0.5145 | 0.5145 | 2.91043 |
| (g:0,3) | 0.83563 | -0.83563 | 2.75744 |
| (g:1,2) | 0.86603 | -0.28868 | 2.85774 |
| (g:2,1) | 0.86603 | 0.28868 | 2.85774 |
| (g:3,0) | 0.83563 | 0.83563 | 2.75744 |
| (g:0,4) | 1.1767 | -1.1767 | 2.49615 |
| (g:1,3) | 1.25109 | -0.62554 | 2.65396 |
| (g:2,2) | 1.2792 | 0 | 2.7136 |
| (g:3,1) | 1.25109 | 0.62554 | 2.65396 |
| (g:4,0) | 1.1767 | 1.1767 | 2.49615 |
| (g:0,5) | 1.5 | -1.5 | 2.12132 |
| (g:1,4) | 1.63663 | -0.98198 | 2.31455 |
| (g:2,3) | 1.72062 | -0.34412 | 2.43332 |
| (g:3,2) | 1.72062 | 0.34412 | 2.43332 |
| (g:4,1) | 1.63663 | 0.98198 | 2.31455 |
| (g:5,0) | 1.5 | 1.5 | 2.12132 |
| (g:0,6) | 1.76505 | -1.76505 | 1.6641 |
| (g:1,5) | 1.96396 | -1.30931 | 1.85164 |
| (g:2,4) | 2.12132 | -0.70711 | 2 |
| (g:3,3) | 2.18282 | 0 | 2.05798 |
| (g:4,2) | 2.12132 | 0.70711 | 2 |
| (g:5,1) | 1.96396 | 1.30931 | 1.85164 |
| (g:6,0) | 1.76505 | 1.76505 | 1.6641 |
| (g:0,7) | 1.9498 | -1.9498 | 1.18176 |
| (g:1,6) | 2.1894 | -1.56386 | 1.32698 |
| (g:2,5) | 2.40887 | -1.03237 | 1.45999 |
| (g:3,4) | 2.54662 | -0.3638 | 1.54349 |
| (g:4,3) | 2.54662 | 0.3638 | 1.54349 |
| (g:5,2) | 2.40887 | 1.03237 | 1.45999 |
| (g:6,1) | 2.1894 | 1.56386 | 1.32698 |
| (g:7,0) | 1.9498 | 1.9498 | 1.18176 |
| (g:0,8) | 2.05798 | -2.05798 | 0.72761 |
| (g:1,7) | 2.3094 | -1.73205 | 0.8165 |
| (g:2,6) | 2.55841 | -1.2792 | 0.90453 |
| (g:3,5) | 2.75299 | -0.68825 | 0.97333 |
| (g:4,4) | 2.82843 | 0 | 1 |
| (g:5,3) | 2.75299 | 0.68825 | 0.97333 |
| (g:6,2) | 2.55841 | 1.2792 | 0.90453 |
| (g:7,1) | 2.3094 | 1.73205 | 0.8165 |
| (g:8,0) | 2.05798 | 2.05798 | 0.72761 |
| (g:0,9) | 2.10835 | -2.10835 | 0.33129 |
| (g:1,8) | 2.35005 | -1.82782 | 0.36927 |
| (g:2,7) | 2.59808 | -1.44338 | 0.40825 |
| (g:3,6) | 2.81494 | -0.93831 | 0.44233 |
| (g:4,5) | 2.94594 | -0.32733 | 0.46291 |
| (g:5,4) | 2.94594 | 0.32733 | 0.46291 |
| (g:6,3) | 2.81494 | 0.93831 | 0.44233 |
| (g:7,2) | 2.59808 | 1.44338 | 0.40825 |
| (g:8,1) | 2.35005 | 1.82782 | 0.36927 |
| (g:9,0) | 2.10835 | 2.10835 | 0.33129 |
| (g:0,10) | 2.12132 | -2.12132 | 0 |
| (g:1,9) | 2.34261 | -1.87409 | 0 |
| (g:2,8) | 2.57248 | -1.54349 | 0 |
| (g:3,7) | 2.78543 | -1.11417 | 0 |
| (g:4,6) | 2.94174 | -0.58835 | 0 |
| (g:5,5) | 3 | 0 | 0 |
| (g:6,4) | 2.94174 | 0.58835 | 0 |
| (g:7,3) | 2.78543 | 1.11417 | 0 |
| (g:8,2) | 2.57248 | 1.54349 | 0 |
| (g:9,1) | 2.34261 | 1.87409 | 0 |
| (g:10,0) | 2.12132 | 2.12132 | 0 |
| (i:0,0) | 0.13811 | 0 | 2.7344 |
| (i:0,1) | 0.37814 | -0.22688 | 2.67386 |
| (i:1,0) | 0.37814 | 0.22688 | 2.67386 |
| (i:0,2) | 0.65654 | -0.49241 | 2.55335 |
| (i:1,1) | 0.66653 | 0 | 2.59218 |
| (i:2,0) | 0.65654 | 0.49241 | 2.55335 |
| (i:0,3) | 0.9619 | -0.78701 | 2.34967 |
| (i:1,2) | 0.99639 | -0.27174 | 2.43391 |
| (i:2,1) | 0.99639 | 0.27174 | 2.43391 |
| (i:3,0) | 0.9619 | 0.78701 | 2.34967 |
| (i:0,4) | 1.26813 | -1.08697 | 2.04961 |
| (i:1,3) | 1.34424 | -0.5761 | 2.17262 |
| (i:2,2) | 1.37296 | 0 | 2.21904 |
| (i:3,1) | 1.34424 | 0.5761 | 2.17262 |
| (i:4,0) | 1.26813 | 1.08697 | 2.04961 |
| (i:0,5) | 1.53987 | -1.35871 | 1.66531 |
| (i:1,4) | 1.66716 | -0.88262 | 1.80297 |
| (i:2,3) | 1.7445 | -0.30785 | 1.8866 |
| (i:3,2) | 1.7445 | 0.30785 | 1.8866 |
| (i:4,1) | 1.66716 | 0.88262 | 1.80297 |
| (i:5,0) | 1.53987 | 1.35871 | 1.66531 |
| (i:0,6) | 1.74891 | -1.57402 | 1.23667 |
| (i:1,5) | 1.92034 | -1.15221 | 1.35789 |
| (i:2,4) | 2.05235 | -0.61571 | 1.45123 |
| (i:3,3) | 2.10308 | 0 | 1.4871 |
| (i:4,2) | 2.05235 | 0.61571 | 1.45123 |
| (i:5,1) | 1.92034 | 1.15221 | 1.35789 |
| (i:6,0) | 1.74891 | 1.57402 | 1.23667 |
| (i:0,7) | 1.88756 | -1.72343 | 0.81243 |
| (i:1,6) | 2.08336 | -1.35871 | 0.8967 |
| (i:2,5) | 2.25558 | -0.88262 | 0.97083 |
| (i:3,4) | 2.36021 | -0.30785 | 1.01586 |
| (i:4,3) | 2.36021 | 0.30785 | 1.01586 |
| (i:5,2) | 2.25558 | 0.88262 | 0.97083 |
| (i:6,1) | 2.08336 | 1.35871 | 0.8967 |
| (i:7,0) | 1.88756 | 1.72343 | 0.81243 |
| (i:0,8) | 1.96633 | -1.81508 | 0.42782 |
| (i:1,7) | 2.16621 | -1.49969 | 0.47131 |
| (i:2,6) | 2.3551 | -1.08697 | 0.5124 |
| (i:3,5) | 2.49645 | -0.5761 | 0.54316 |
| (i:4,4) | 2.54978 | 0 | 0.55476 |
| (i:5,3) | 2.49645 | 0.5761 | 0.54316 |
| (i:6,2) | 2.3551 | 1.08697 | 0.5124 |
| (i:7,1) | 2.16621 | 1.49969 | 0.47131 |
| (i:8,0) | 1.96633 | 1.81508 | 0.42782 |
| (i:0,9) | 2.00257 | -1.86446 | 0.09766 |
| (i:1,8) | 2.19322 | -1.58819 | 0.10695 |
| (i:2,7) | 2.37997 | -1.23102 | 0.11606 |
| (i:3,6) | 2.53592 | -0.78701 | 0.12367 |
| (i:4,5) | 2.62684 | -0.27174 | 0.1281 |
| (i:5,4) | 2.62684 | 0.27174 | 0.1281 |
| (i:6,3) | 2.53592 | 0.78701 | 0.12367 |
| (i:7,2) | 2.37997 | 1.23102 | 0.11606 |
| (i:8,1) | 2.19322 | 1.58819 | 0.10695 |
| (i:9,0) | 2.00257 | 1.86446 | 0.09766 |
| (g:0,0)-(i:0,0) (g:0,10)-(i:0,9) (g:10,0)-(i:9,0) | 3 | 0.29936 |
| (g:0,0)-(g:0,1) (g:0,0)-(g:1,0) (g:0,9)-(g:0,10) (g:0,10)-(g:1,9) (g:9,0)-(g:10,0) (g:9,1)-(g:10,0) | 6 | 0.3318 |
| (i:0,0)-(i:0,1) (i:0,0)-(i:1,0) (i:0,8)-(i:0,9) (i:0,9)-(i:1,8) (i:8,0)-(i:9,0) (i:8,1)-(i:9,0) | 6 | 0.33579 |
| (g:0,1)-(i:0,1) (g:1,0)-(i:1,0) (g:0,9)-(i:0,8) (g:9,0)-(i:8,0) (g:1,9)-(i:1,8) (g:9,1)-(i:8,1) | 6 | 0.33984 |
| (g:0,1)-(i:0,0) (g:1,0)-(i:0,0) (g:0,9)-(i:0,9) (g:9,0)-(i:9,0) (g:1,9)-(i:0,9) (g:9,1)-(i:9,0) | 6 | 0.35391 |
| (g:0,1)-(g:1,1) (g:1,0)-(g:1,1) (g:0,9)-(g:1,8) (g:8,1)-(g:9,0) (g:1,8)-(g:1,9) (g:8,1)-(g:9,1) | 6 | 0.37224 |
| (i:0,1)-(i:1,1) (i:1,0)-(i:1,1) (i:0,8)-(i:1,7) (i:7,1)-(i:8,0) (i:1,7)-(i:1,8) (i:7,1)-(i:8,1) | 6 | 0.37592 |
| (g:0,2)-(i:0,2) (g:2,0)-(i:2,0) (g:0,8)-(i:0,7) (g:8,0)-(i:7,0) (g:2,8)-(i:2,7) (g:8,2)-(i:7,2) | 6 | 0.38492 |
| (g:1,1)-(i:0,1) (g:1,1)-(i:1,0) (g:1,8)-(i:1,8) (g:1,8)-(i:0,8) (g:8,1)-(i:8,1) (g:8,1)-(i:8,0) | 6 | 0.38837 |
| (g:1,1)-(i:1,1) (g:1,8)-(i:1,7) (g:8,1)-(i:7,1) | 3 | 0.38971 |
| (g:0,2)-(i:0,1) (g:2,0)-(i:1,0) (g:0,8)-(i:0,8) (g:8,0)-(i:8,0) (g:2,8)-(i:1,8) (g:8,2)-(i:8,1) | 6 | 0.39658 |
| (g:0,1)-(g:0,2) (g:1,0)-(g:2,0) (g:0,8)-(g:0,9) (g:8,0)-(g:9,0) (g:1,9)-(g:2,8) (g:8,2)-(g:9,1) | 6 | 0.40266 |
| (i:0,1)-(i:0,2) (i:1,0)-(i:2,0) (i:0,7)-(i:0,8) (i:7,0)-(i:8,0) (i:1,8)-(i:2,7) (i:7,2)-(i:8,1) | 6 | 0.40315 |
| (g:0,2)-(g:1,2) (g:2,0)-(g:2,1) (g:0,8)-(g:1,7) (g:7,1)-(g:8,0) (g:2,7)-(g:2,8) (g:7,2)-(g:8,2) | 6 | 0.42112 |
| (g:1,2)-(i:0,2) (g:2,1)-(i:2,0) (g:1,7)-(i:0,7) (g:7,1)-(i:7,0) (g:2,7)-(i:2,7) (g:7,2)-(i:7,2) | 6 | 0.42195 |
| (i:0,2)-(i:1,2) (i:2,0)-(i:2,1) (i:0,7)-(i:1,6) (i:6,1)-(i:7,0) (i:2,6)-(i:2,7) (i:6,2)-(i:7,2) | 6 | 0.42244 |
| (g:0,3)-(i:0,3) (g:3,0)-(i:3,0) (g:0,7)-(i:0,6) (g:7,0)-(i:6,0) (g:3,7)-(i:3,6) (g:7,3)-(i:6,3) | 6 | 0.42963 |
| (g:0,3)-(i:0,2) (g:3,0)-(i:2,0) (g:0,7)-(i:0,7) (g:7,0)-(i:7,0) (g:3,7)-(i:2,7) (g:7,3)-(i:7,2) | 6 | 0.43763 |
| (g:1,2)-(i:1,1) (g:2,1)-(i:1,1) (g:1,7)-(i:1,7) (g:7,1)-(i:7,1) (g:2,7)-(i:1,7) (g:7,2)-(i:7,1) | 6 | 0.44006 |
| (g:1,2)-(i:1,2) (g:2,1)-(i:2,1) (g:1,7)-(i:1,6) (g:7,1)-(i:6,1) (g:2,7)-(i:2,6) (g:7,2)-(i:6,2) | 6 | 0.44375 |
| (g:1,3)-(i:0,3) (g:3,1)-(i:3,0) (g:1,6)-(i:0,6) (g:6,1)-(i:6,0) (g:3,6)-(i:3,6) (g:6,3)-(i:6,3) | 6 | 0.44977 |
| (i:0,1)-(i:1,0) (i:0,8)-(i:1,8) (i:8,0)-(i:8,1) | 3 | 0.45377 |
| (i:1,1)-(i:1,2) (i:1,1)-(i:2,1) (i:1,6)-(i:1,7) (i:1,7)-(i:2,6) (i:6,1)-(i:7,1) (i:6,2)-(i:7,1) | 6 | 0.45574 |
| (g:1,1)-(g:1,2) (g:1,1)-(g:2,1) (g:1,7)-(g:1,8) (g:1,8)-(g:2,7) (g:7,1)-(g:8,1) (g:7,2)-(g:8,1) | 6 | 0.45916 |
| (g:0,4)-(i:0,4) (g:4,0)-(i:4,0) (g:0,6)-(i:0,5) (g:6,0)-(i:5,0) (g:4,6)-(i:4,5) (g:6,4)-(i:5,4) | 6 | 0.46455 |
| (g:1,4)-(i:0,4) (g:4,1)-(i:4,0) (g:1,5)-(i:0,5) (g:5,1)-(i:5,0) (g:4,5)-(i:4,5) (g:5,4)-(i:5,4) | 6 | 0.46584 |
| (g:0,4)-(i:0,3) (g:4,0)-(i:3,0) (g:0,6)-(i:0,6) (g:6,0)-(i:6,0) (g:4,6)-(i:3,6) (g:6,4)-(i:6,3) | 6 | 0.46845 |
| (g:0,1)-(g:1,0) (g:0,9)-(g:1,9) (g:9,0)-(g:9,1) | 3 | 0.46852 |
| (i:0,2)-(i:0,3) (i:2,0)-(i:3,0) (i:0,6)-(i:0,7) (i:6,0)-(i:7,0) (i:2,7)-(i:3,6) (i:6,3)-(i:7,2) | 6 | 0.47066 |
| (i:0,3)-(i:1,3) (i:3,0)-(i:3,1) (i:0,6)-(i:1,5) (i:5,1)-(i:6,0) (i:3,5)-(i:3,6) (i:5,3)-(i:6,3) | 6 | 0.47118 |
| (g:0,3)-(g:1,3) (g:3,0)-(g:3,1) (g:0,7)-(g:1,6) (g:6,1)-(g:7,0) (g:3,6)-(g:3,7) (g:6,3)-(g:7,3) | 6 | 0.47692 |
| (g:0,5)-(i:0,5) (g:0,5)-(i:0,4) (g:5,0)-(i:5,0) (g:5,0)-(i:4,0) (g:5,5)-(i:4,5) (g:5,5)-(i:5,4) | 6 | 0.47906 |
| (g:0,2)-(g:0,3) (g:2,0)-(g:3,0) (g:0,7)-(g:0,8) (g:7,0)-(g:8,0) (g:2,8)-(g:3,7) (g:7,3)-(g:8,2) | 6 | 0.47923 |
| (g:2,2)-(i:1,2) (g:2,2)-(i:2,1) (g:2,6)-(i:2,6) (g:2,6)-(i:1,6) (g:6,2)-(i:6,2) (g:6,2)-(i:6,1) | 6 | 0.48172 |
| (g:1,3)-(i:1,2) (g:3,1)-(i:2,1) (g:1,6)-(i:1,6) (g:6,1)-(i:6,1) (g:3,6)-(i:2,6) (g:6,3)-(i:6,2) | 6 | 0.48833 |
| (g:1,3)-(i:1,3) (g:3,1)-(i:3,1) (g:1,6)-(i:1,5) (g:6,1)-(i:5,1) (g:3,6)-(i:3,5) (g:6,3)-(i:5,3) | 6 | 0.49275 |
| (i:0,2)-(i:1,1) (i:1,1)-(i:2,0) (i:0,7)-(i:1,7) (i:7,0)-(i:7,1) (i:1,7)-(i:2,7) (i:7,1)-(i:7,2) | 6 | 0.49404 |
| (g:2,2)-(i:2,2) (g:2,6)-(i:2,5) (g:6,2)-(i:5,2) | 3 | 0.50337 |
| (i:1,2)-(i:2,2) (i:2,1)-(i:2,2) (i:0,4)-(i:1,4) (i:0,5)-(i:1,4) (i:4,0)-(i:4,1) (i:4,1)-(i:5,0) (i:1,6)-(i:2,5) (i:5,2)-(i:6,1) (i:2,5)-(i:2,6) (i:5,2)-(i:6,2) (i:4,4)-(i:4,5) (i:4,4)-(i:5,4) | 12 | 0.51168 |
| (g:2,3)-(i:1,3) (g:3,2)-(i:3,1) (g:2,5)-(i:1,5) (g:5,2)-(i:5,1) (g:3,5)-(i:3,5) (g:5,3)-(i:5,3) | 6 | 0.51326 |
| (g:0,2)-(g:1,1) (g:1,1)-(g:2,0) (g:0,8)-(g:1,8) (g:8,0)-(g:8,1) (g:1,8)-(g:2,8) (g:8,1)-(g:8,2) | 6 | 0.51641 |
| (g:1,4)-(i:1,3) (g:4,1)-(i:3,1) (g:1,5)-(i:1,5) (g:5,1)-(i:5,1) (g:4,5)-(i:3,5) (g:5,4)-(i:5,3) | 6 | 0.51998 |
| (g:1,4)-(i:1,4) (g:4,1)-(i:4,1) (g:1,5)-(i:1,4) (g:5,1)-(i:4,1) (g:4,5)-(i:4,4) (g:5,4)-(i:4,4) | 6 | 0.52204 |
| (i:0,3)-(i:1,2) (i:2,1)-(i:3,0) (i:0,3)-(i:0,4) (i:3,0)-(i:4,0) (i:0,5)-(i:0,6) (i:5,0)-(i:6,0) (i:0,6)-(i:1,6) (i:6,0)-(i:6,1) (i:2,6)-(i:3,6) (i:3,6)-(i:4,5) (i:5,4)-(i:6,3) (i:6,2)-(i:6,3) | 12 | 0.52325 |
| (g:1,2)-(g:2,2) (g:2,1)-(g:2,2) (g:1,7)-(g:2,6) (g:6,2)-(g:7,1) (g:2,6)-(g:2,7) (g:6,2)-(g:7,2) | 6 | 0.52424 |
| (g:2,4)-(i:1,4) (g:4,2)-(i:4,1) (g:4,4)-(i:4,4) | 3 | 0.52525 |
| (i:0,4)-(i:1,3) (i:1,2)-(i:1,3) (i:2,1)-(i:3,1) (i:3,1)-(i:4,0) (i:0,5)-(i:1,5) (i:5,0)-(i:5,1) (i:1,5)-(i:1,6) (i:5,1)-(i:6,1) (i:2,6)-(i:3,5) (i:5,3)-(i:6,2) (i:3,5)-(i:4,5) (i:5,3)-(i:5,4) | 12 | 0.53095 |
| (g:0,4)-(g:1,4) (g:4,0)-(g:4,1) (g:0,6)-(g:1,5) (g:5,1)-(g:6,0) (g:4,5)-(g:4,6) (g:5,4)-(g:6,4) | 6 | 0.53145 |
| (g:2,3)-(i:2,2) (g:3,2)-(i:2,2) (g:2,5)-(i:2,5) (g:5,2)-(i:5,2) (g:3,5)-(i:2,5) (g:5,3)-(i:5,2) | 6 | 0.53405 |
| (i:1,2)-(i:2,1) (i:0,4)-(i:0,5) (i:4,0)-(i:5,0) (i:1,6)-(i:2,6) (i:6,1)-(i:6,2) (i:4,5)-(i:5,4) | 6 | 0.54348 |
| (g:2,3)-(i:2,3) (g:3,2)-(i:3,2) (g:2,5)-(i:2,4) (g:5,2)-(i:4,2) (g:3,5)-(i:3,4) (g:5,3)-(i:4,3) | 6 | 0.54844 |
| (g:0,3)-(g:0,4) (g:3,0)-(g:4,0) (g:0,6)-(g:0,7) (g:6,0)-(g:7,0) (g:3,7)-(g:4,6) (g:6,4)-(g:7,3) | 6 | 0.54857 |
| (g:1,2)-(g:1,3) (g:2,1)-(g:3,1) (g:1,6)-(g:1,7) (g:6,1)-(g:7,1) (g:2,7)-(g:3,6) (g:6,3)-(g:7,2) | 6 | 0.55071 |
| (g:0,3)-(g:1,2) (g:2,1)-(g:3,0) (g:0,7)-(g:1,7) (g:7,0)-(g:7,1) (g:2,7)-(g:3,7) (g:7,2)-(g:7,3) | 6 | 0.5569 |
| (i:1,3)-(i:2,3) (i:3,1)-(i:3,2) (i:1,5)-(i:2,4) (i:4,2)-(i:5,1) (i:3,4)-(i:3,5) (i:4,3)-(i:5,3) | 6 | 0.56033 |
| (g:2,4)-(i:2,4) (g:2,4)-(i:2,3) (g:4,2)-(i:4,2) (g:4,2)-(i:3,2) (g:4,4)-(i:3,4) (g:4,4)-(i:4,3) | 6 | 0.56059 |
| (g:3,3)-(i:2,3) (g:3,3)-(i:3,2) (g:3,4)-(i:3,4) (g:3,4)-(i:2,4) (g:4,3)-(i:4,3) (g:4,3)-(i:4,2) | 6 | 0.56238 |
| (g:0,5)-(g:1,4) (g:4,1)-(g:5,0) (g:0,5)-(g:1,5) (g:5,0)-(g:5,1) (g:4,5)-(g:5,5) (g:5,4)-(g:5,5) | 6 | 0.56952 |
| (g:3,3)-(i:3,3) (g:3,4)-(i:3,3) (g:4,3)-(i:3,3) | 3 | 0.57642 |
| (g:1,2)-(g:2,1) (g:1,7)-(g:2,7) (g:7,1)-(g:7,2) | 3 | 0.57735 |
| (g:0,4)-(g:1,3) (g:3,1)-(g:4,0) (g:0,6)-(g:1,6) (g:6,0)-(g:6,1) (g:3,6)-(g:4,6) (g:6,3)-(g:6,4) | 6 | 0.57811 |
| (i:1,3)-(i:2,2) (i:2,2)-(i:3,1) (i:1,3)-(i:1,4) (i:3,1)-(i:4,1) (i:1,4)-(i:1,5) (i:4,1)-(i:5,1) (i:1,5)-(i:2,5) (i:5,1)-(i:5,2) (i:2,5)-(i:3,5) (i:3,5)-(i:4,4) (i:4,4)-(i:5,3) (i:5,2)-(i:5,3) | 12 | 0.57868 |
| (i:1,4)-(i:2,3) (i:2,2)-(i:2,3) (i:2,2)-(i:3,2) (i:3,2)-(i:4,1) (i:1,4)-(i:2,4) (i:4,1)-(i:4,2) (i:2,4)-(i:2,5) (i:2,5)-(i:3,4) (i:4,2)-(i:5,2) (i:4,3)-(i:5,2) (i:3,4)-(i:4,4) (i:4,3)-(i:4,4) | 12 | 0.58594 |
| (g:1,3)-(g:2,3) (g:3,1)-(g:3,2) (g:1,6)-(g:2,5) (g:5,2)-(g:6,1) (g:3,5)-(g:3,6) (g:5,3)-(g:6,3) | 6 | 0.5902 |
| (g:0,4)-(g:0,5) (g:4,0)-(g:5,0) (g:0,5)-(g:0,6) (g:5,0)-(g:6,0) (g:4,6)-(g:5,5) (g:5,5)-(g:6,4) | 6 | 0.59123 |
| (i:2,3)-(i:3,2) (i:2,3)-(i:2,4) (i:3,2)-(i:4,2) (i:2,4)-(i:3,4) (i:3,4)-(i:4,3) (i:4,2)-(i:4,3) | 6 | 0.61571 |
| (i:2,3)-(i:3,3) (i:2,4)-(i:3,3) (i:3,2)-(i:3,3) (i:3,3)-(i:4,2) (i:3,3)-(i:3,4) (i:3,3)-(i:4,3) | 6 | 0.61883 |
| (g:1,3)-(g:1,4) (g:3,1)-(g:4,1) (g:1,5)-(g:1,6) (g:5,1)-(g:6,1) (g:3,6)-(g:4,5) (g:5,4)-(g:6,3) | 6 | 0.62521 |
| (g:2,2)-(g:2,3) (g:2,2)-(g:3,2) (g:2,5)-(g:2,6) (g:2,6)-(g:3,5) (g:5,2)-(g:6,2) (g:5,3)-(g:6,2) | 6 | 0.62596 |
| (g:1,3)-(g:2,2) (g:2,2)-(g:3,1) (g:1,6)-(g:2,6) (g:6,1)-(g:6,2) (g:2,6)-(g:3,6) (g:6,2)-(g:6,3) | 6 | 0.62901 |
| (g:1,4)-(g:2,4) (g:1,5)-(g:2,4) (g:4,1)-(g:4,2) (g:4,2)-(g:5,1) (g:4,4)-(g:4,5) (g:4,4)-(g:5,4) | 6 | 0.63986 |
| (g:1,4)-(g:2,3) (g:3,2)-(g:4,1) (g:1,5)-(g:2,5) (g:5,1)-(g:5,2) (g:3,5)-(g:4,5) (g:5,3)-(g:5,4) | 6 | 0.65423 |
| (g:1,4)-(g:1,5) (g:4,1)-(g:5,1) (g:4,5)-(g:5,4) | 3 | 0.65465 |
| (g:2,3)-(g:3,3) (g:3,2)-(g:3,3) (g:2,5)-(g:3,4) (g:4,3)-(g:5,2) (g:3,4)-(g:3,5) (g:4,3)-(g:5,3) | 6 | 0.6877 |
| (g:2,3)-(g:3,2) (g:2,5)-(g:3,5) (g:5,2)-(g:5,3) | 3 | 0.68825 |
| (g:2,3)-(g:2,4) (g:3,2)-(g:4,2) (g:2,4)-(g:2,5) (g:4,2)-(g:5,2) (g:3,5)-(g:4,4) (g:4,4)-(g:5,3) | 6 | 0.69288 |
| (g:2,4)-(g:3,3) (g:3,3)-(g:4,2) (g:2,4)-(g:3,4) (g:4,2)-(g:4,3) (g:3,4)-(g:4,4) (g:4,3)-(g:4,4) | 6 | 0.71214 |
| (g:3,3)-(g:3,4) (g:3,3)-(g:4,3) (g:3,4)-(g:4,3) | 3 | 0.72761 |
The vrml world for this example displays a patch which looks like this:
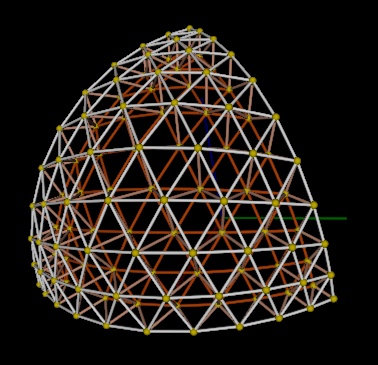
The octahedron has the qualities of a geodesic: its equilateral triangular basis makes it strong, it uses materials more efficiently that traditional architectures, and as the tessellation frequency increases it more and more closely approaches its limiting circumscribed sphere. Its projected patches bulge more than the icosahedral geodesic, but less than the tetrahedral geodesic. This is expected since each patch covers an eighth of a sphere to the tetrhedral's fourth and the icosahedral's twentieth.
 However, the truly useful quality of the octahedral geodesic is that it aligns with the traditional architectural forms.
Although an octahedral geodesic dome can certainly stand alone, it can also be joined directly as geodesic living space to an existing rectangular box structure.
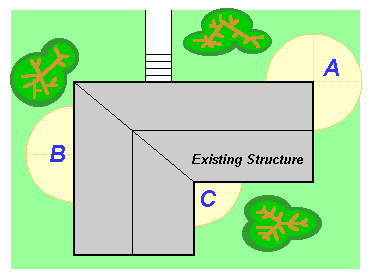
Consider a residence as pictured; sections of an octahedral, half-spherical geodesic may be attached to the structure simply and directly since it can be fabricated in 90o sections.
In A, 3/4 of the dome is attached to extend a corner.
In B, 1/2 of the dome is attached to join to a side.
In C, 1/4 of the dome is attached as a fill-in between two sides at a corner.
These extensions could be connected to an existing structure relatively easily, bringing homes built in the past forward into the geodesic age.
However, the truly useful quality of the octahedral geodesic is that it aligns with the traditional architectural forms.
Although an octahedral geodesic dome can certainly stand alone, it can also be joined directly as geodesic living space to an existing rectangular box structure.
Consider a residence as pictured; sections of an octahedral, half-spherical geodesic may be attached to the structure simply and directly since it can be fabricated in 90o sections.
In A, 3/4 of the dome is attached to extend a corner.
In B, 1/2 of the dome is attached to join to a side.
In C, 1/4 of the dome is attached as a fill-in between two sides at a corner.
These extensions could be connected to an existing structure relatively easily, bringing homes built in the past forward into the geodesic age.
There are many places where rectangular box construction could be augmented by the spherical dome, as anyone interested in geodesics knows. However, few can afford the luxury of leveling their house or place of business to construct the more efficient geodesic structure - and few builders are up to the task of pure geodesic construction. If prefabricated octahedral geodesic sections could be shipped to a site, assembled into a right-angle-fitting unit, and attached directly onto the structure, the benefits of geodesic living could be mainstreamed perhaps a little more quickly.