David Anderson
Originally written in February 1998
After writing some simple code to generate geodesic angles and lengths (follow links from here), the time had come to temper the calculations with a little reality. It was time to build prototypical models.
Easy to say, especially with all the math done, but what do you use as materials? You need struts and hubs. In a large world, struts should be rigid and hubs have to be strong and shear-resistant; everything is measured and cut precisely as time has been taken to make sure the cost of materials isn't wasted. In my small, modeling world, struts should still be rigid, but hubs need to be flexible and forgiving since the precision is not as imperitive as simply being able to try new ideas quickly.
After some cursory searching on the web, I found that I'd need to be creative and figure out a technique that would work for me, since I couldn't find anybody who really talks about the specifics of building geodesic models out there...
Everybody is entitled to at least one false start.
A trip to the local craft store netted me a thousand popsicle sticks, a spool of 20 guage wire, and a spool of 30 guage wire. Calculating a two frequency icosahedral geodesic dome for a maximum subface edge length of 4.1 inches (the useable length of the ubiquitous popsicle stick) I got out a drill and saw and made lots of the two sizes of struts I'd need. I drilled a hole at each end of the stick making sure the distance between the holes matched the calculated chord length of the strut.
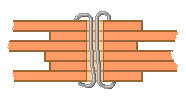The wire was used to tie together five or six sticks at a vertex.
I decided to stack the sticks at a vertex since this seemed easy to do, and the wires could be tightened if the structure seemed "flimsy".
Several sticks would be brought together, their holes aligned, and a wire looped around and through a couple times.
The ends of the wire would be twisted together; more tension on the twist would serve to tighten up the stack and make the geodesic more rigid locally.
I made more than I needed since I figured the quality of the wood wasn't great and I'd be wiring the struts together. Under tension, The wire could cut through the cheap wood. If that happened, I'd not only have to rewire the vertex with the damaged strut, but also the adjoining vertex connected by the damaged strut; but I figured I'd only have to do that a few times since the wood wasn't that cheap.
But I was wrong.
The different height of sticks at a vertex caused some serious problems. There was as much as a half inch effective difference in actual versus intended chord length at some vertices. In a larger structure, this would be a problem, but not a big one since the as the strut lengthens the relative error decreases. But half an inch of error doesn't diminish very much on a four inch strut; the dome was distorted and as it grew, so did the tension on individual vertices which translated to twisting and bending of the popsicle sticks. Each additional vertex caused a bit more distortion and sticks started to be cut by wires. At about a 40% of a sphere, I decided it was only going to get worse. My first attempt is now hanging on a wall in the basement with several struts just about at their limit.
Of course, since I had so many popsicle sticks I figured, what the heck, I'd try again. Tight vertices seemed like the problem: I decided to loosen them up a little. Instead of using wire, I'd try something with a little more give. So, I went out and bought some string.
Now, the nice thing about wire is that you can push it through a hole. Wire stays rigid; generally an intentional effort is required to bend a piece of wire. String doesn't act so nicely. No matter how hard you try, you can't push a string through a small hole - it must be dragged. I got a big needle, threaded it with the string, and started dragging.
After about twenty minutes I had three sticks strung together. At this rate it'd take weeks to build the model. Seeing as I didn't want to spend weeks on just the first of many models, I decided a new way must be found. The remainder of the sticks became kindling.
I sent out a quick note requesting a scalable design for hubs from the folks on the geodesic mailing list. I got a couple of responses (and I thank all who replied) but nothing seemed like it was what I was looking for; they all took to much effort. I needed something quick-and-dirty. Fortunately I had included access to my other geodesic papers in my mail message.
John Dunaj, another geodesic modeler, took a look at the calculation papers and wrote back, saying the chord length tables had helped his planning; he was using plastic soda straws and small nuts and bolts. Plastic straws! That was the answer for the strut - rigid enough, easy to cut to length, and cheap. But using screws for hubs was too high-maintenance and expensive for me. I wanted to be able to build a model, strip down a section, and replace it with framing for windows or doors - or whatever. I needed hubs that would facilitate attaching together hollow cylinders of varying length.
Then the answer for quick, low cost hubs hit me...
Pipe cleaners make the perfect hub! You can twist a few pipe cleaners together to form a five-spoked or six-spoked star, fold the ends over a few times so they'll plug in the straws, cut the straws to the right length (taking away a tenth of an inch or so for the pipe cleaner fuzz factor), and you're set!
By making the pipe cleaners stick down the straws a good fraction of their length, a dome model predicated on this technique stands up very well for design purposes. A section of the dome may extracted, quickly modified, and replaced - all to give the model a plug-and-play quality that was very attractive to the quick-and-dirty designer in me.
Of course, other qualities of the geodesic are not realized. Most seriously: a force applied on a strut, once it becomes great enough to overcome the coefficient of friction between a plastic straw and a pipe cleaner, causes the struts to slip on the hubs. In a bolted model, this would not happen: the structure would become stronger (unless the local force-time differential is great enough to break a bolt or strut - all real materials have their limits.)
However, when I'm considering a model for a structure I intend to build, I'm not looking at proving physical properties - I'm simply interested that I crunched the numbers correctly and that the results look good to me. For geodesic domes, I take it for granted that structural engineers know what they're talking about: geodesic structures are the ephemeral in Fuller's sense of the word: they give the most for the least. I simply assume if the materials are good and the frequency is right, the dome will be strong.
I built a 14" diameter icosahedron first, to test different pipe cleaner twisting and folding techniques. Total time: about an hour.
I built a 19" diameter semi-spherical 2-frequency geodesic dome, cutting the straws and forming the hubs as I went along. Total time: about an hour and a half.
I built a 36.5" diameter semi-spherical 4-frequency geodesic dome, pre-cutting all the struts and pre-making all the hubs before I started assembly. Total time: about 4 hours.
And, to give my son something he could think about and play with, I built a tetrahedron with 4" struts.. Total time: about 5 minutes.
The 2-frequency dome is destined to become a 15' diameter greenhouse this spring or summer; I'll probably use bolts and PVC pipe, and cover the thing with plastic, clear on all the sunlit exposures, but internally reflective on the north side. I'll put a door on the north side and have a couple of quick-change screen sections so I can use it in summer and winter.
The 4-frequency dome is destined to become a 35' diamter patio enclosure, basically to keep the elements away from some areas on the patio. This dome may become multi-frequency: some faces may be tesselated at a higher frequency than others. Some of this will be based on functional need: the patio is used as a basketball half-court and should keep the ball from rolling escaping down the hill next to the patio - a tighter tesselation will keep the basketball in. Some of this will be based on design need: the enclosure will be anchored to the ground around the patio and also to bricks on the house. It is likely to be hemispherical (or a little more) with a third (or so) of the dome sliced off to accomodate the house, and some open holes on the sides at strategic places to let people use existing walkways.
By playing with a model based on the quick-and-dirty platic straw and pipe cleaner technique, I should be able to get things going much more quickly on each project than I would if I had to rely on pure mathematics. And since I'll be able to play more than calculate, the end results should feel much more playful than a purely calculated space.