David Anderson
Originally written in July 1999
Geodesic domes are fun, geodesic domes are cool. But they are not the only geodesic structures based on projection.
Domes are formulated on the different platonic solids, the twenty-sided icosahedron, the eight-sided octahedron, and the four-sided tetrahedron. The faces of these structures are equilateral triangles - each is divided into a mesh of smaller equilateral triangles. When the vertices of these subfaces are all projected on to sphere that circumscribes the solid, the result is a geodesic structure.
I approached the creation of these structures through geodesic patches: one tesselated face of the solid is created, replicated, and then is placed edge-to-edge around a vertex to form the surface of the solid. There are three around a vertex for the tetrahedral geodesic, four for the octahedral, and five for the icosahedral. As the number of number of subfaces that the face is divided into increases, when they are projected the figures more and more closely approach their circumscribing spheres.
With the addition of the concepts of projection parameterization, which gave us superprojection and subprojection, and the creation of the blending function, which enabled us to join differently projected patches and alter the shapes of patch surfaces, a different universe of geodesic-based forms has been created. What was formerly simple spherical projection has now evolved into regularly-generated, but bizarre, geometry.
This patch-based construction is valid for geodesic structures based on the tetrahedron, octahedron, and icosahedron. The patches are all based on tesselating equilateral triangles: the edges of equilateral faces are kept in place by the blending function. We've previously projected them onto the circumscribing sphere and then applied the blending function to hold them in place during the application of the projection parameter. They need not be held to the sphere; the edges of the faces can be projected onto any surface prior to application of the blending function.
One of the important parts of building geodesic structures is that they generally need to sit on a flat surface. Each of the platonic-based geodesics and be divided on such a way that it can sit naturally on a plane; this can happen either by slicing through certain vertices on the geodesic, or by slicing through other vertices and sides, and distorting the surface.
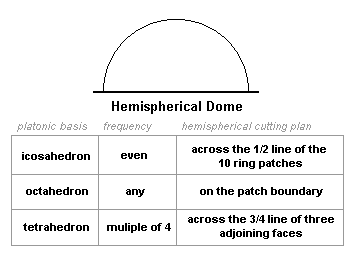For instance, a natural hemispherical geodesic can be realized by cutting along given edges of platonics with a certain frequency.
From the notes in the diagram, an icosahedron of even frequency can be divided into two equal halves along a great circle; an octahedral half is simply four patches with a common vertex; and the multiple-of-four frequency tetrahedron can be naturally cleaved by cutting 3/4 of the way down three patches with a common vertex.
The tetrahedral case is even more interesting because the two halves are not symmetric: one has a single patch vertex at the top of the dome, while the other has three vertices spaced evenly around the dome, a little up from the bottom.
In all of these, the bottoms are naturally flat; and since this is an angular phenomenon, not a scaling one, patches with different projection characteristics but that are still based on the same underlying solid and frequency from the table will still have a flat base.
Since we have worked out the projection mathematics and blending functions for a patch, there is another way to get a geodesic-projection-based flat patch: we can simply use the blending function prior to the spherical projection. This will keep the edges of the equilateral face flat. Such a face will have a triangular footprint, but can be made with all the same strength and materials properties as a part of a geodesic dome, complete with warped octet truss structures.
For example, the model on the right is a flat-edged icosahedral patch with a simple third-order polynomial blending function modifying a projection parameter. This is augmented with a warped octet truss. The structure has a flat triangular base, rises steeply at the center of the sides, and flattens nicely for most of its span. (Click the picture to bring up a VRML world without the external truss.)
This kind of enclosure reminds me very much of a covered stadium - it exhibits a strong structural framework over a large unobstructed area. The truss system would be particularly effective for snowy areas where the load would challenge many conventional structures. The frequency here has been kept low for file-size purposes, but if it were pushed up to thirty, the curves would be much more gradual and the truss profile would be lower.
Flat-edged patches are a different sort of geodesic form. Made up of equilateral trianglular tesselations which are projected outward onto a surface, they are an animal in the same family; simpler than a dome, but exhibiting many features which are important for construction in the large.
I'm not saying that cities of the future will have their transitways laid out in a triangular mesh with patch structures in the blocks, but then again, who knows...