David Anderson
Originally written in January 1998
When building a geodesic structure there are a many ways to go.
If the intention is to do something human-scaled, it all boils down whether you want to go with traditional or non-traditional materials.
For instance, how do you fasten struts together in a 5-frequency geodesic without a special hub?
A set of pre-manufactured aluminum joints is wonderful - but where do you get them?
Although these kinds of special parts have their advantages, for me, being able to just go down to the local hardware store or lumber yard is a bigger win.
I don't want to have to worry about ordering special parts for something I'm building when I could take a short drive instead.
I don't know, I'm just funny that way.
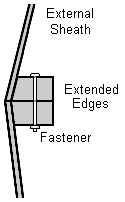
Assuming a human-scaled structure, the icosahedral geodesic can be framed by joining prefabricated triangular subfaces made of standard materials whose edges are extended and angled in such a way that they lie flat against each other and can be fastened together. I call these edge angles fastening angles; they vary according to the position of the subface on the geodesic patch.
With the determination of chord lengths completed, I proceeded onward to figure out the geometry of the subfaces making up a geodesic.
Using the reference vertex layout for a geodesic patch (in this case, 4-frequency)
The various subfaces of the patch may be found by walking the mesh. The first three coefficients for the equation of the plane (Ax+By+Cz-D=0) the subface lies in are also calculated (which are the unnormalized direction cosines of the normal to the plane.)
| Vertices | Chords | Direction Coefficients | ||
| A | B | C | ||
| (0,0) (0,1) (1,0) | 0.24079 0.28079 0.24079 | 0.00855 | 0.0 | 0.05425 |
| (0,1) (0,2) (1,1) | 0.28397 0.29755 0.28011 | 0.02639 | -0.01111 | 0.06528 |
| (0,1) (1,1) (1,0) | 0.28011 0.28011 0.28079 | 0.01963 | 0.0 | 0.06516 |
| (1,0) (1,1) (2,0) | 0.28011 0.29755 0.28397 | 0.02639 | 0.01111 | 0.06528 |
| (0,2) (0,3) (1,2) | 0.28397 0.28011 0.29755 | 0.04098 | -0.02171 | 0.05414 |
| (0,2) (1,2) (1,1) | 0.29755 0.30901 0.29755 | 0.04131 | -0.01223 | 0.06571 |
| (1,1) (1,2) (2,1) | 0.30901 0.30901 0.30901 | 0.05020 | 0.0 | 0.06571 |
| (1,1) (2,1) (2,0) | 0.30901 0.29755 0.29755 | 0.04131 | 0.01223 | 0.06571 |
| (2,0) (2,1) (3,0) | 0.29755 0.28011 0.28397 | 0.04098 | 0.02171 | 0.05414 |
| (0,3) (0,4) (1,3) | 0.24079 0.24079 0.28079 | 0.03971 | -0.02263 | 0.03045 |
| (0,3) (1,3) (1,2) | 0.28079 0.28011 0.28011 | 0.04819 | -0.02074 | 0.04335 |
| (1,2) (1,3) (2,2) | 0.28011 0.28397 0.29755 | 0.05628 | -0.01059 | 0.04245 |
| (1,2) (2,2) (2,1) | 0.29755 0.29755 0.30901 | 0.05815 | 0.0 | 0.05285 |
| (2,1) (2,2) (3,1) | 0.29755 0.28397 0.28011 | 0.05628 | 0.01059 | 0.04245 |
| (2,1) (3,1) (3,0) | 0.28011 0.28079 0.28011 | 0.04819 | 0.02074 | 0.04335 |
| (3,0) (3,1) (4,0) | 0.28079 0.24079 0.24079 | 0.03971 | 0.02263 | 0.03045 |
Here the vertices (and chord lengths) of the subface are calculated in a counter-clockwise direction. By inspection it can be seen that rotational symmetry is evident with respect to the placement of a subface in the mesh. However, moving from the center of the mesh outwards, some subfaces are mirror images of others. If a patch is being constructed with different inside and outside materials, the handedness of the subface matters. In the case of edge extensions for fastening, the handedness must be observed.
Rather than calculate the dihedral angle along and edge between subfaces, the dihedral angle between the subface and the plane including the edge and the icosahedral center (an edge plane) is calculated (the fastening angle.) Two subfaces which share a common edge are fastened together along their edge plane when each is angled by its fastening angle.
The fastening angle is calculated by computing the direction coefficients of the edge plane and then determining the dihedral angle between them.
| Vertices | Edge | Fastening Angle | |
| radians | degrees | ||
| (0,0) (0,1) (1,0) | (0,0) (0,1) | 1.47908 | 84.74502 |
| (0,1) (1,0) | 1.52035 | 87.10942 | |
| (1,0) (0,0) | 1.47908 | 84.74502 | |
| (0,1) (0,2) (1,1) | (0,1) (0,2) | 1.47922 | 84.75287 |
| (0,2) (1,1) | 1.49233 | 85.50421 | |
| (1,1) (0,1) | 1.47593 | 84.56438 | |
| (0,1) (1,1) (1,0) | (0,1) (1,1) | 1.48445 | 85.05278 |
| (1,1) (1,0) | 1.48445 | 85.05278 | |
| (1,0) (0,1) | 1.48507 | 85.08838 | |
| (1,0) (1,1) (2,0) | (1,0) (1,1) | 1.47593 | 84.56438 |
| (1,1) (2,0) | 1.49233 | 85.50421 | |
| (2,0) (1,0) | 1.47922 | 84.75287 | |
| (0,2) (0,3) (1,2) | (0,2) (0,3) | 1.47922 | 84.75287 |
| (0,3) (1,2) | 1.47593 | 84.56438 | |
| (1,2) (0,2) | 1.49233 | 85.50421 | |
| (0,2) (1,2) (1,1) | (0,2) (1,2) | 1.47441 | 84.47770 |
| (1,2) (1,1) | 1.48522 | 85.09681 | |
| (1,1) (0,2) | 1.47441 | 84.47770 | |
| (1,1) (1,2) (2,1) | (1,1) (1,2) | 1.47559 | 84.54528 |
| (1,2) (2,1) | 1.47559 | 84.54528 | |
| (2,1) (1,1) | 1.47559 | 84.54528 | |
| (1,1) (2,1) (2,0) | (1,1) (2,1) | 1.48522 | 85.09681 |
| (2,1) (2,0) | 1.47441 | 84.47770 | |
| (2,0) (1,1) | 1.47441 | 84.47770 | |
| (2,0) (2,1) (3,0) | (2,0) (2,1) | 1.49233 | 85.50421 |
| (2,1) (3,0) | 1.47593 | 84.56438 | |
| (3,0) (2,0) | 1.47922 | 84.75287 | |
| (0,3) (0,4) (1,3) | (0,3) (0,4) | 1.47908 | 84.74502 |
| (0,4) (1,3) | 1.47908 | 84.74502 | |
| (1,3) (0,3) | 1.52035 | 87.10942 | |
| (0,3) (1,3) (1,2) | (0,3) (1,3) | 1.48507 | 85.08838 |
| (1,3) (1,2) | 1.48445 | 85.05278 | |
| (1,2) (0,3) | 1.48445 | 85.05278 | |
| (1,2) (1,3) (2,2) | (1,2) (1,3) | 1.47593 | 84.56438 |
| (1,3) (2,2) | 1.47922 | 84.75287 | |
| (2,2) (1,2) | 1.49233 | 85.50421 | |
| (1,2) (2,2) (2,1) | (1,2) (2,2) | 1.47441 | 84.47770 |
| (2,2) (2,1) | 1.47441 | 84.47770 | |
| (2,1) (1,2) | 1.48522 | 85.09681 | |
| (2,1) (2,2) (3,1) | (2,1) (2,2) | 1.49233 | 85.50421 |
| (2,2) (3,1) | 1.47922 | 84.75287 | |
| (3,1) (2,1) | 1.47593 | 84.56438 | |
| (2,1) (3,1) (3,0) | (2,1) (3,1) | 1.48445 | 85.05278 |
| (3,1) (3,0) | 1.48507 | 85.08838 | |
| (3,0) (2,1) | 1.48445 | 85.05278 | |
| (3,0) (3,1) (4,0) | (3,0) (3,1) | 1.52035 | 87.10942 |
| (3,1) (4,0) | 1.47908 | 84.74502 | |
| (4,0) (3,0) | 1.47908 | 84.74502 | |
Note that the dihedral angle between the two subfaces is the sum of their common edge's two fastening angles.
Here are the fastening angle calculations for the first five tesselations for an icosahedral patch:
and here's a coffeescript app to generate the fastening angles for an arbitrary frequency.