
Visualizing the Bulge in Geodesic Projections
David Anderson
Originally written in July 1998
A few folks have sent me mail asking me what I meant by the difference in bulges encountered in geodesic projections.
I claimed the icosahedral geodesic bulged less than the octahedral, which in turn bulged less than the tetrahedral.
The idea is that since all points on the geodesic sphere must be an equal distance from the center, a geodesic based on a polyhedron with fewer tesselated sides must bulge more since the subfaces at center of the side must be projected further to reach the geodesic sphere.
A reasonable bulge factor probably could therefore be defined as the distance the center of the side had to be projected divided by the area of the side.
Since all of the primitives we're considering have sides which are equilateral triangles, for a side with a length of 1 the area is 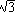 /4.
This gives a bulge factor of 0.451 for the icoshedron, 0.691 for the octahedron, and 0.943 for the terahedron.
Taken this way, the octahedral projection makes bulges 53% more than the icosahedral projection, and the tetrahedral projection 110% more than the icosahedral and 45% more than the octahedral projections.
/4.
This gives a bulge factor of 0.451 for the icoshedron, 0.691 for the octahedron, and 0.943 for the terahedron.
Taken this way, the octahedral projection makes bulges 53% more than the icosahedral projection, and the tetrahedral projection 110% more than the icosahedral and 45% more than the octahedral projections.
To visually demonstrate this amount of bulge, I created three series of VRML files, each based on a different primitive, featuring green and yellow balls.
The red-green-blue axis gives the a reference to the VRML X-Y-Z directions respectively.
In each world, the set of green balls make up the unprojected mesh which constitutes an n-frequency side of the underlying primitive.
The centers of these balls align on the mesh.
The centers of the set of yellow balls lie on the geodesic, projected in a straight line from the center of the primitive.
In addition to all this, the size of each of the yellow balls has been scaled in direct proportion to the distance they were projected to reach the sphere.
So, if this helps you visualize what is meant by bulge, great.
If not, then simply enjoy the graphics.
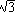 /4.
This gives a bulge factor of 0.451 for the icoshedron, 0.691 for the octahedron, and 0.943 for the terahedron.
Taken this way, the octahedral projection makes bulges 53% more than the icosahedral projection, and the tetrahedral projection 110% more than the icosahedral and 45% more than the octahedral projections.
/4.
This gives a bulge factor of 0.451 for the icoshedron, 0.691 for the octahedron, and 0.943 for the terahedron.
Taken this way, the octahedral projection makes bulges 53% more than the icosahedral projection, and the tetrahedral projection 110% more than the icosahedral and 45% more than the octahedral projections.
